SOLUTION: SinB=-1/2, 3pi/2 < B < 2pi; sinC= 1/4, pi/2 < C < pi find tan(B+C)

,  
 

First we draw angles B and C is standard position.

3pi/2 < B < 2pi means QIV. So we draw an angle with terminal side 
in QIV and assume the angle indicated by the red arc is theta:

 

Then we draw a perpendicular (in green) up to the x-axis from the 
end of the terminal side of B.  That makes a right triangle with 
the x-axis.



We know that the sine of B is -1/2.  We also know that the sine is 
the opposite over the hypotenuse, so we make the opposite side (the 
green side) equal to the numerator of -1/2, which is -1, (negative, 
since it goes downward). And we make the hypotenuse (the terminal
side of B) be 2 (positive because the terminal side is always taken 
positive).  Then we calculate the adjacent side on the x-axis by the 
Pythagorean theorem:






And since the adjacent side goes to the right of the origin we take
the positive square root,




--------

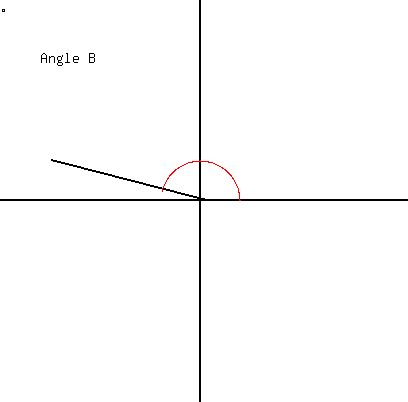
pi/2 < C < pi means QII. So we draw an angle with terminal side 
in QII and assume the angle indicated by the red arc is C:

 

Then we draw a perpendicular (in green) down to the x-axis from the 
end of the terminal side of C.  That makes a right triangle with 
the x-axis.



We know that the sine of B is 1/4.  We also know that the sine is the 
opposite over the hypotenuse, so we make the opposite side (the green 
side) equal to the numerator of 1/4, which is 1, (positive, since it 
goes up). And we make the hypotenuse (the terminal side of B) be 4 
(since the terminal side is always taken positive).  Then we calculate 
the adjacent side on the x-axis by the Pythagorean theorem:






And since the adjacent side goes to the left of the origin we take
the negative square root,




Now we have both angles A and B, so now we can proceed to finding
tan(A+B)


   






Multiply every term by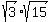 



Rationalize the denominator by multiplying by 










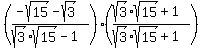
Edwin

1.  Since sin(B) =   and since B is the angle in QIV, where cosine is positive, we have

        cos(B) =  =  =  = ;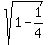

        hence,  tan(B) =  =  = .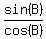



2.  Since sin(C) =   and since C is the angle in QII, where cosine is negative, we have

        cos(C) =  =  =  = ;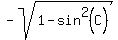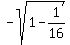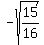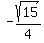

        hence,  tan(C) =  =  = .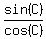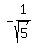



3.  Now apply the formula for tangent of sum

        tan(B+C) =  = .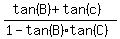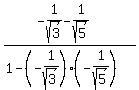


     At this point, we have the same formula as Edwin has in his post, and further simplifications can be done by the same way as Edwin did.