SOLUTION: Show without a calculator that: 2arccos(3/4) = arcsin[3sqrt(7)/8]

Show without a calculator that:

2arccos(3/4) = arcsin[3sqrt(7)/8]

let  and  

Then , 

The problem becomes to show this:



We draw 2 right triangles with angle  in one and
angle  in the other.

Since the cosine is the adjacent over the hypotenuse, we put the numerator
of the cosine of alpha, which is 3, on the adjacent side of alpha, and the
denominator of the cosine, which is 4, on the hypotenuse.

Since the sine is the opposite over the hypotenuse, we put the numerator
of the sine of beta, which is 3sqrt(7), on the opposite side of beta, and
the denominator of the cosine, which is 8, on the hypotenuse.

Then we calculate the third side in each by the Pythagorean theorem:

  
  

To show:



We show that the cosine of the left equals the right side.



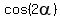We use 








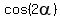
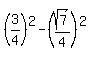
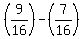
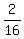
And as we see from the second triangle, .

Edwin

Let a = .


Then  cos(a) = .  and  since   > ,  the angle "a" is less than  ,  so the angle 2a is in QI.


Therefore,  sin(a) =  =  =  =  = .


Then sin(2a) = 2*sin(a)*cos(a) =  = .


Thus the angles  2a  and    have the same value of sine function and both are in Q1;


hence,  2a = ,  or   = ,


QED.