SOLUTION: consider x^3 − kx + (k + 11) = 0 Use long division to show that k = x^2 + x + 1 + 12/(x-1)

When we divide polynomials we write the answer



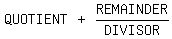So QUOTIENT = 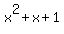, REMAINDER = 12, DIVISOR = x-1,

we know that we are to divide by x-1

             x² +       x +    (-k+1) 
x - 1) x³ + 0x² -      kx +    (k+11)
       x³ -  x² 
             x² -      kx
             x² -       x 
                  (-k+1)x +    (k+11)
                  (-k+1)x -    (-k+1)
                            (k+11)+(-k+1) = k+11-k+1 = 12


I get the remainder 12, but the last term in the quotient
is (-k+1), whereas the last term in the quotient you gave
was 1.  Did you leave out the -k?  Or does it mean that -k+1 = 1
and k = 0.  If k = 0, then the long division becomes


             x² +  x +  1
x - 1) x³ + 0x² - 0x + 11
       x³ -  x² 
             x² - 0x
             x² -  x 
                   x + 11
                   x -  1
                       12

Edwin