Question 1143226: Box A contains nine cards numbered 1 through 9,and box B contains five cards numbered 1 through 5. A box is chosen at random and a card is drawn. If the number is even find the probability that the card came from Box A.
Found 2 solutions by 4419875, ikleyn:
Answer by 4419875(21)   (Show Source): (Show Source):
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Box A contains nine cards numbered 1 through 9,and box B contains five cards numbered 1 through 5.
A box is chosen at random and a card is drawn. If the number is even find the probability that the card came from Box A.
~~~~~~~~~~~~~~~~~~~~
The solution by the other post answers the question:
What is the probability to get an even number from box A ?
But the question in the problem is TOTALLY DIFFERENT, so that solution is IRRELEVANT.
Below find the correct solution.
By the definition, the conditional probability is
P(A) = P(even,A)/P(even,A+B),
where P(A) is the probability under the question that the number came from box A provided that it is even;
P(even,A) is the probability to get even number from box A;
P(even,A+B) is the probability to get even number from either box A or box B.
Box A contains 9 numbers; of them, 4 numbers are even.
Box B contains 5 numbers; of them, 2 numbers are even.
Therefore, we have
P(even,A+B) =  = = 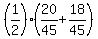 = =  ;
P(even,A) = ;
P(even,A) = 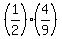 .
Therefore,
P(A) = .
Therefore,
P(A) =  = = 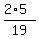 = = 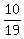 = 0.5263 = 52.63% (approximately). ANSWER = 0.5263 = 52.63% (approximately). ANSWER
|
|
|