Question 1143050: A jet airplane departing on time, flying between two airports at an average speed of 540 mph
arrives eight minutes late. Departing on time and flying at an average speed of 480 mph it
arrives fifty-three minutes late. What is the number of miles between the two airports?
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A jet airplane departing on time, flying between two airports at an average speed of 540 mph
arrives eight minutes late. Departing on time and flying at an average speed of 480 mph it
arrives fifty-three minutes late. What is the number of miles between the two airports?
=====================
d = distance
---
A jet airplane departing on time, flying between two airports at an average speed of 540 mph arrives eight minutes late.
t1 = time at 540 mi/hr
t1 = d/540
=================
Departing on time and flying at an average speed of 480 mph it arrives fifty-three minutes late.
t2 = time at 480 mi/hr
t2 = d/480
=============================
t2 = t1 + 0.75 ----- time in hours
d/480 = d/540 + 0.75
----
Solve for d.
---
Email via the TY note for help, or to check your work.
Answer by ikleyn(52818)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let d be the distance between the two airports (in miles).
Flying at the speed of 540 mph, the airplane spends 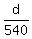 hours and arrives 8 minutes later.
Flying at the speed of 480 mph, the airplane spends hours and arrives 8 minutes later.
Flying at the speed of 480 mph, the airplane spends 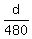 hours and arrives 53 minutes later.
The difference of times is hours and arrives 53 minutes later.
The difference of times is 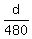 - - 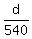 hours.
From the other side, this difference is 53-8 = 45 minutes = hours.
From the other side, this difference is 53-8 = 45 minutes =  of an hour = of an hour =  of an hour.
It gives you the "time" equation of an hour.
It gives you the "time" equation
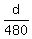 - - 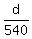 = =  .
At this point, the setup is just completed.
To find "d", multiply both sides of the equation (1) by 60. You will get .
At this point, the setup is just completed.
To find "d", multiply both sides of the equation (1) by 60. You will get
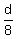 - -  = 45.
One more time, multiply both sides of the last equation by 72. You will get
9d - 8d = 72*45,
d = 3240
ANSWER. The distance between the two airports is 3240 miles.
CHECK. = 45.
One more time, multiply both sides of the last equation by 72. You will get
9d - 8d = 72*45,
d = 3240
ANSWER. The distance between the two airports is 3240 miles.
CHECK. 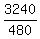 = 6.75 hours; = 6.75 hours;
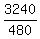 = 6 hours.
The difference is 0.75 of an hour = = 6 hours.
The difference is 0.75 of an hour =  of an hour -- ! Correct ! of an hour -- ! Correct !
----------------
Using "time" equation is the STANDARD method of solving such problems.
It is simple, logical, straightforward and economic. Going in this way, you will not make a mistake - the logic of the method
prevents you of making mistakes.
From this lesson, learn on how to write, how to use and how to solve a "time" equation.
To see many other similar solved problems, look into the lessons
- Had a car move faster it would arrive sooner
- How far do you live from school? (*)
- Earthquake waves
- Time equation: HOW TO use, HOW TO write and HOW TO solve it
in this site.
For the TWIN problem, see the lesson (*) in the list.
|
|
|