SOLUTION: A ferris wheel is 60 meters in diameter and boarded at its lowest point (6 O'Clock) from a platform which is 6 meters above ground. The wheel makes one full rotation every 18 minut

(a)  Middle line of the function h = f(t) = the height of the center of the ferris wheel = 6 + 60/2 = 6 + 30 = 36 meters.



(b)  The period of rotation is 18 minutes; so the wheel turns 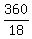  = 20 degrees per minute.


     The condition does not say if the wheel rotates clockwise or anti-clockwise.


     If it rotates clockwise, the current angle is   = 270 - 20*t degrees, where t is the time in minutes.


     Then the height function  h = f(t) =  = .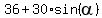



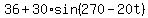     If the wheel rotates anti-clockwise, the current angle is   = 270 + 20*t degrees.


     Then the height function  h = g(t) =  = .



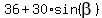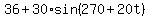     If you look into these height functions, you will see that actually 


        f(t) = g(t)


    independently of the direction of rotation. So, in both cases


        h = f(t) = 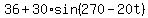 = g(t) = .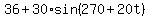