.
The full space of events is the set of all pairs (i,j), where i and j are integer numbers from 1 to 6, inclusively.
This space consists of 6*6 = 36 elements, and each element/event has the probability of  .
Of them, the outcomes where the sum is 2 or 12, are
sum 2 : (1,1) In all, 1 pair worth $20.
sum 12 : (6,6) In all, 1 pair worth $20.
The outcomes where the product is 12, are
(2,6), (3,4), (4,3), (6,2) In all, 4 pairs worth $15 each
The outcomes where the sum is 5 or 9, are
sum 5 : (1,4), (2,3), (3,2), (4,1) In all, 4 pairs worth $2 each
sum 9 : (3,6), (4,5), (5,4), (6,3) In all, 4 pairs worth $2 each
Thus the mathematical expectation of winning sum is
.
Of them, the outcomes where the sum is 2 or 12, are
sum 2 : (1,1) In all, 1 pair worth $20.
sum 12 : (6,6) In all, 1 pair worth $20.
The outcomes where the product is 12, are
(2,6), (3,4), (4,3), (6,2) In all, 4 pairs worth $15 each
The outcomes where the sum is 5 or 9, are
sum 5 : (1,4), (2,3), (3,2), (4,1) In all, 4 pairs worth $2 each
sum 9 : (3,6), (4,5), (5,4), (6,3) In all, 4 pairs worth $2 each
Thus the mathematical expectation of winning sum is
 =
= 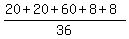 =
= 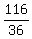 =
= 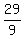 =
= 
 dollars.
ANSWER. For the game to be fair, the person should pay
dollars.
ANSWER. For the game to be fair, the person should pay 
 dollars.
dollars.