Question 1142773: Train A travels 10km/h faster than Train B. These trains travel from area 1 to area 2 which are 100km apart. Train B travels 30 minutes longer than train A to cover the same distance. What is the speed of train B?
Found 2 solutions by math_helper, ikleyn:
Answer by math_helper(2461)   (Show Source): (Show Source):
Answer by ikleyn(52908)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
When students solve such problems, the major difficulty is to setup a governing equation.
I will show you a standard and straightforward way to do it.
Let r be the rate of train B, in kilometers per hour (the unknown value under the question).
Then the rate of the train A is (r+10) km/h, according to the condition.
Train's B traveling time is 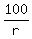 hours.
Train's A traveling time is hours.
Train's A traveling time is 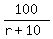 hours.
The difference of traveling times is hours.
The difference of traveling times is  of an hour, according to the condition.
It gives you this "time" equation of an hour, according to the condition.
It gives you this "time" equation
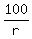 - - 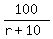 = =  hours. <<<---=== Every fraction on the left side is the traveling time . . .
At this point, the setup is just completed (!)
To solve the equation, multiply both sides by 2*r*(r+10). You will get
200*(r+10) - 200*r = r*(r+10)
2000 = r^2 + 10r
r^2 + 10r - 2000 = 0
(r+50)*(r-40) = 0
The two roots of the equation are r = -50 and r = 40, but only positive r = 40 km/h makes sense and is the solution to the problem.
ANSWER. The rate of train B is 40 kilometers per hour.
CHECK. Travel time for train A is hours. <<<---=== Every fraction on the left side is the traveling time . . .
At this point, the setup is just completed (!)
To solve the equation, multiply both sides by 2*r*(r+10). You will get
200*(r+10) - 200*r = r*(r+10)
2000 = r^2 + 10r
r^2 + 10r - 2000 = 0
(r+50)*(r-40) = 0
The two roots of the equation are r = -50 and r = 40, but only positive r = 40 km/h makes sense and is the solution to the problem.
ANSWER. The rate of train B is 40 kilometers per hour.
CHECK. Travel time for train A is  = =  = 2 hours;
Travel time for train B is = 2 hours;
Travel time for train B is 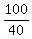 = =   hours, which is 30 minutes longer than that of train A. ! Correct ! hours, which is 30 minutes longer than that of train A. ! Correct !
Solved
Using "time" equation is the STANDARD way to solve such problems.
From this solution, learn on how to write, how to use and how to solve a "time" equation.
---------------
To see many other similar solved problems, look into the lessons
- Had a car move faster it would arrive sooner
- How far do you live from school?
- Earthquake waves
- Time equation: HOW TO use, HOW TO write and HOW TO solve it
in this site.
|
|
|