Question 1142768:
Suppose that you received an unexpected inheritance of $36,000. You have decided to invest the money by placing some of the money in stocks that pay 4.4% and the rest in bonds that pay 6%. How much should you place in each investment in order to earn 5%, or $1800 annually?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52852)   (Show Source):
You can put this solution on YOUR website! .
Let x = the amount invested at 4.4% and y = the amount invested at 6%.
Then from the condition you have these two equations in two unknowns
x + y = 36000 dollars (1) (total investment)
0.044x + 0.06y = 1800 dollars (2) (total interest)
Solve the system by the Substitution method.
For it, from equation (1) express x = 36000 - y and substitute it into equation (2). You will get
0.044*(36000-y) + 0.06y = 1800
Simplify and express y from the last equation; then calculate
y = 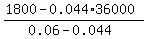 = 13500.
To find x, substitute the found value of y into equation (1). You will get then
x = 36000 - 13500 = 22500.
ANSWER. $22500 was invested at 4.4% and $13500 was invested at 6%.
CHECK. 0.044*22500 + 0.06*13500 = 1800 dollars. ! Correct !
Solved.
-------------------
It is a typical and standard problem on investment.
To see many other similar solved problems on investment, look into the lesson
- Using systems of equations to solve problems on investment
in this site.
You will find there different approaches (using one equation or a system of two equations in two unknowns), as well as
different methods of solution to the equations (Substitution, Elimination).
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
Here is an alternative method for solving "mixture" problems like this that will get you to the answer much faster, and with far less effort, than the traditional algebraic method shown by the other tutor.
(1) The overall percent return, 5%, is 3/8 of the way from 4.4% to 6%. (4.4 to 6 is a difference of 1.6; 4.4 to 5 is a difference of .6; .6/1.6 = 6/16 = 3/8).
(2) That means 3/8 of the money should be invested at the higher rate.
ANSWER: 3/8 of $36,000, or $13,500, at 6%; the other $22,500 at 4.4%.
CHECK: .06(13,500)+.044(22,500) = 810+990 = 1800
|
|
|
