Question 1142726: **Solve using calculus optimization**
A company that produces chemicals used in manufacturing sells a certain product for $200 per unit. The total production cost for the product is
C(x)= 500,000 + 80x + 0.003x^2
The company can produce no more than 30,000 units during a given time period. How
many units of the chemical product should be manufactured and sold to maximize profit?
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A company that produces chemicals used in manufacturing sells a certain product for $200 per unit. The total production cost for the product is
C(x)= 500,000 + 80x + 0.003x^2
The company can produce no more than 30,000 units during a given time period. How
many units of the chemical product should be manufactured and sold to maximize profit?
--------------
It's a parabola with a minimum.
C(x)= 500,000 + 80x + 0.003x^2
C'(x) = 80 + 0.006x = 0
x = 80/0/006 = 13,333 units
Answer by ikleyn(52772)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The PROFIT function P(x) is the difference REVENUE - COST
P(x) = 200x - (500000+80x+0.003x^2) = -0.003x^2 + 120x - 500000. (1)
This quadratic function plot is opened downward, so it has the maximum.
The maximum of a quadratic function is achieved at x =  (referring to the general form f(x) = ax^2 + bx + c).
In our case " a " = -0.003, b = 120, so the maximum is achieved at x = (referring to the general form f(x) = ax^2 + bx + c).
In our case " a " = -0.003, b = 120, so the maximum is achieved at x = 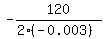 = = 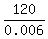 = 20000.
It is LESS than the company capacity of 30000.
So, the company profit will be maximum at x = 20000.
The profit value is then = 20000.
It is LESS than the company capacity of 30000.
So, the company profit will be maximum at x = 20000.
The profit value is then
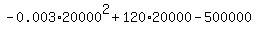 = 700,000.
ANSWER. 20,000 units should be manufactured and sold. = 700,000.
ANSWER. 20,000 units should be manufactured and sold.
-----------------
On finding the maximum/minimum of a quadratic function see the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Finding minimum/maximum of quadratic functions".
================
Sorry, in my solution I used the standard Algebra approach instead of Calculus.
But you will get the same answer, using Calculus.
For it, simply differentiate the quadratic function P(x) (formula (1)) and equate the derivative to zero
P'(x) = -0.003*2*x + 120 = 0
120 = 0.006x
x = 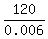 = 20000. ANSWER = 20000. ANSWER
Solved. // So, now you have both Algebra and Calculus solutions.
|
|
|