Question 1142647: A bag contains 2 red, 4 green, and 5 yellow m&m. Find the probability of drawing at least one green m&m. Write answer as a fraction.
Answer by ikleyn(52887)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A bag contains 2 red, 4 green, and 5 yellow m&m. Find the probability of drawing at least one green m&m. Write answer as a fraction.
~~~~~~~~~~~~~~~~~
As the problem is printed, written, posted and presented, it MAKES NO SENSE.
To be correct, the formulation should point on HOW MANY m&m's are taken off (= are drawn out) at a time .
-------------
comment from student: A bag contains 2 red, 4 green, and 5 yellow m&m. Two are randomly drawn in succession, without replacement.
Find the probability of drawing at least one green m&m. Write answer as a fraction.
-------------
My response :
O ! This corrected formulation totally changes everything !
Now it is a good, reasonable and fine Math problem.
The solutions is as follows.
To solve the problem, let's consider the complement set of events.
The complement set of events is to get no one green m&m when drawing randomly two m&m in succession.
It means that selection is made, actually, among the subset of 2 red and 5 yellow m&m.
This subset contains 2+5 = 7 m&m's, and the number of different pairs among them is  = = 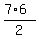 = 21.
The total number of different pairs of m&m's in the whole set of 2 red, 4 green, and 5 yellow m&m is = 21.
The total number of different pairs of m&m's in the whole set of 2 red, 4 green, and 5 yellow m&m is
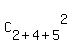 = = 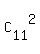 = = 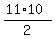 = 55.
So, the probability of not getting a green m&m is = 55.
So, the probability of not getting a green m&m is 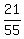 .
Therefore, the complement probability to get at least one m&m is
1 - .
Therefore, the complement probability to get at least one m&m is
1 - 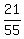 = = 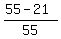 = = 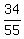 . ANSWER . ANSWER
Solved.
|
|
|