|
Question 1142603: Two college students have started their own business building computers from kits. Working alone, one student can build a computer in 20 hours. When the second student helps, they can build a computer in 7.5 hours. How long would it take the second student, working alone to build the computer? create and equation and solve
Found 3 solutions by ankor@dixie-net.com, ikleyn, greenestamps:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Two college students have started their own business building computers from kits.
Working alone, one student can build a computer in 20 hours.
When the second student helps, they can build a computer in 7.5 hours.
How long would it take the second student, working alone to build the computer?
create and equation and solve
:
let x = the time required by the 2nd student alone
let the completed job = 1
:
Each will do a fraction of the job, the two fractions add up to 1
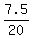 + + 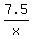 = 1 = 1
multiply by 20x, cancel the denominators
7.5x + 20(7.5) = 20x
7.5x + 150 = 20x
150 = 20x - 7.5x
150 = 12.5x
x = 150/12.5
x = 12 hrs required by the 2nd student alone
Answer by ikleyn(52946)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I will tell you about two ways of solving such problems.
The first way is to make an equation and then to solve it.
Here it is.
Let t be the time (in hours) for the second student to complete the job, working alone.
Since the first student can make the entire job, working alone, in 20 hours, he makes  of the job per hour.
Since the second student can make the entire job, working alone, in t hours, he makes of the job per hour.
Since the second student can make the entire job, working alone, in t hours, he makes 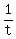 of the job per hour.
Working together, the two students make of the job per hour.
Working together, the two students make  + + 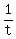 of the job per hour.
From the other side, we know from the condition, that working together, the two students make the job in 7.5 hours --
hence, they make of the job per hour.
From the other side, we know from the condition, that working together, the two students make the job in 7.5 hours --
hence, they make  part of the job per hour.
It gives you an equation part of the job per hour.
It gives you an equation
 + + 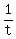 = =  .
At this point the setup is completed: the equation is constructed, and your next step is to solve it.
For it, multiply both sides by 60t to rid off the denominators. You will get
3t + 60 = 8t.
Simplify and solve for t :
60 = 8t - 3t
60 = 5t
t = 60/5 = 12.
Thus the problem is just solved, and you just got the
ANSWER : The second student needs 12 hours to complete the job working alone. .
At this point the setup is completed: the equation is constructed, and your next step is to solve it.
For it, multiply both sides by 60t to rid off the denominators. You will get
3t + 60 = 8t.
Simplify and solve for t :
60 = 8t - 3t
60 = 5t
t = 60/5 = 12.
Thus the problem is just solved, and you just got the
ANSWER : The second student needs 12 hours to complete the job working alone.
The second way is to solve the problem WITHOUT making an equation.
Manipulating fractions is ENOUGH.
Here it is.
Working together, the two students make the job in 7.5 hours.
Hence, in one hour (in each hour) they make  of the entire job.
You also are given that the first student can make the entire job in 20 hours, working alone.
It means that he makes of the entire job.
You also are given that the first student can make the entire job in 20 hours, working alone.
It means that he makes  of the job per hour.
Hence, the second student make the rest of the job per hour.
Hence, the second student make the rest  - -  of the job per hour. of the job per hour.
 - -  = =  - -  = =  - -  = = 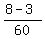 = =  = =  of the job per hour.
It means that the second student will complete the entire job in 12 hours, working alone. of the job per hour.
It means that the second student will complete the entire job in 12 hours, working alone.
You got the same answer.
Now you know TWO WAYS to solve the problem.
--------------------
It is a standard and typical joint work problem.
There is a wide variety of similar solved joint-work problems with detailed explanations in this site. See the lessons
- Using Fractions to solve word problems on joint work
- Solving more complicated word problems on joint work
- Selected joint-work word problems from the archive
Read them and get be trained in solving joint-work problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic
"Rate of work and joint work problems" of the section "Word problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13219)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The other tutor has provided a good response showing the traditional algebraic method for solving this kind of "working together" problem.
The problem as posed appears to require an algebraic solution. However, when a problem like this does not require an algebraic solution, here is an alternative method you can use that I find many students like better.
(1) Consider a common multiple of the two given times.
(2) The LCM of 7.5 and 20 is 60. 7.5*8 = 60; 20*3 = 60.
(3) In 60 hours, the one student alone can build 3 of the computers; in 60 hours the two of them together can build 8 of them.
(4) So the other student can build 5 of the computers in 60 hours; that means he can build 1 computer in 60/5 = 12 hours.
|
|
|
| |