Question 1142582: Suppose a local symphony decides to raise money by raffling off a microwave oven
worth $200, a dinner for two worth $100, and 4 books worth $20 each, total of 1000
tickets are sold at $1 each. Find the expected value of winning for a person who buys
1 ticket in the raffle.
Found 3 solutions by greenestamps, ikleyn, Edwin McCravy:
Answer by greenestamps(13215)   (Show Source):
You can put this solution on YOUR website!
--------------------------------------------------------------
Response edited after re-reading the problem as having one $100 prize instead of two
----------------------------------------------------------------
1 winning ticket worth $200; expected value to ticket holder $200-$1 = $199
2 winning tickets worth $100 each; 1 winning ticket worth $100; expected value to ticket holder $100-$1 = $99
4 winning tickets worth $20 each; expected value to ticket holders $20-1 = $19
994 tickets worth nothing; expected value to ticket holders -$1
Expected value for one ticket:
That was with a straightforward use of the formal definition of expected value.
Here is an easier way to find the answer for this particular type of expected value problem:
Total cost of the 1000 tickets at $1 each: $1000
Total value of the prizes: $200 + $100 + 4*$20 = $380
Expected value of one ticket: $380/1000 = $0.38
"Expected" (actual) cost of ticket: $1.00
Expected value of winning for 1 ticket: $0.38 - $1.00 = -$0.62
Answer by ikleyn(52908)  (Show Source):
You can put this solution on YOUR website! .
Suppose a local symphony decides to raise money by raffling off a microwave oven
worth $200,
a dinner for two worth $100, and 4 books worth $20 each, total of 1000
tickets are sold at $1 each.
Find the expected value of winning for a person who buys 1 ticket in the raffle.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let me note some positions in the problem formulation, that seem to be questionable to me and need to be clarified:
1. Is my understanding correct that the "dinner for two worth $100" goes as the winning prize for 1 ticket only
(and not for 2 tickets, as @greenestamps suggests) ?
2. Is my understanding correct that the "dinner for two" is worth $100, and not $200, as @greenestamps suggest ?
3. Are 4 books at the price of $20 each FOUR different prizes for 4 tickets or just ONE prize for 1 ticket ?
Please respond.
Thank you.
/\/\/\/\/\/\/\/
Dear Edwin,
I got your question to me in the comment section.
Thank you for asking.
I do not think that your solution to this problem is (was) correct.
The repeating experiment, which is behind this problem, is taking one (ONE) ticket at the beginning of each game,
and, therefore, calculation of the Math expectation is performed as it is done by @greenestamps in his corrected solution.
Again, thank you for asking.
You are one of the best tutors in this forum: knowledgeable; accurate; your tone is always adequate
and always in perfect equilibrium with the environment.
Answer by Edwin McCravy(20065)  (Show Source):
You can put this solution on YOUR website! I agree with Ikelyn that the dinner for two is 1 prize. So there are 6
prizes. But I think they will draw the 6 winning tickets one by one without
replacement. So I think it should be this:
which is about -62 cents.
Or we could do it easier by first finding the expectation as if the tickets were free
and then subtracting the $1 paid for the ticket.
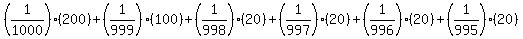That comes out to about 38 cents. So when we subtract the $1 we get about -62 cents.
Edwin
|
|
|
