|
Question 1142489: Hi Please help me.
1. The depth d of a liquid in a bottle with a hole of area 0.5 cm2 in its side can be approximated by
d = 0.0034t2 − 0.52518t + 20,
where t is the time since a stopper was removed from the hole. When will the depth be 1 cm? Round to the nearest tenth of a second.
2. A small pipe can fill a tank in 9 min more time than it takes a larger pipe to fill the same tank. Working together, the pipes can fill the tank in 6 min. How long would it take each pipe, working alone, to fill the tank?
3. A car travels 238 mi. A second car, traveling 9 mph faster than the first car, makes the same trip in 1 h less time. Find the speed of each car.
4. A homeowner hires a mason to lay a brick border around a rectangular patio that measures 8 ft by 10 ft. If the total area of the patio and border is 168 ft2, what is the width of the border?
Found 2 solutions by ikleyn, Alan3354:
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1. d = 0.0034t2 − 0.52518t + 20.
To find " t " when the depth "d" is equal to 1 cm, you need to solve the quadratic equation
0.0034t2 − 0.52518t + 20 = 1.
To solve this equation, first write it in the standard form and then use the quadratic formula.
If you don't know how to use the quadratic formula, learn it from the lessons
- Introduction into Quadratic Equations
- PROOF of quadratic formula by completing the square
in this site.
2. Let " t " be the time for the larger pipe to fill the tank working alone.
Then the time to fill the tank for the smaller pipe is (t+9) minutes.
Now, in one minute the larger pipe fills 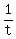 of the tank volume;
the smaller pipe fills of the tank volume;
the smaller pipe fills 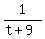 of the tank volume.
Working together, the two pipes fill of the tank volume.
Working together, the two pipes fill 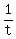 + + 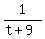 of the tank volume per minute.
From the other side, the two pipes, working together, fill of the tank volume per minute.
From the other side, the two pipes, working together, fill  of the tank volume, according to the condition.
It gives you an equation of the tank volume, according to the condition.
It gives you an equation
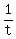 + + 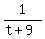 = =  .
To solve it, multiply both sides by 6t*(t+9). You will get
6(t+9) + 6t = t*(t+9).
Transform this equation to the standard form
6t + 54 + 6t = t^2 + 9t
t^2 - 3t - 54 = 0
Now you can solve it by factoring
(t-9)*(t+6) = 0.
It has two roots t= -6 and t= 9.
Of these two roots, only positive t= 9 is the valid solution to the problem.
ANSWER. Large pipe can fill the tank in 9 minutes, working alone.
Small pipe can fill the tank in (9+9) = 18 minutes.
CHECK. .
To solve it, multiply both sides by 6t*(t+9). You will get
6(t+9) + 6t = t*(t+9).
Transform this equation to the standard form
6t + 54 + 6t = t^2 + 9t
t^2 - 3t - 54 = 0
Now you can solve it by factoring
(t-9)*(t+6) = 0.
It has two roots t= -6 and t= 9.
Of these two roots, only positive t= 9 is the valid solution to the problem.
ANSWER. Large pipe can fill the tank in 9 minutes, working alone.
Small pipe can fill the tank in (9+9) = 18 minutes.
CHECK.  + +  = = 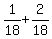 = = 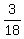 = =  . ! Correct ! . ! Correct !
--------------
The rule of this forum is THIS :
ONE and ONLY ONE problem per post.
Do not put more than one problem into your posts.
If you do it, you CAN NOT expect to get full scale solutions to each of your problem, and the tutors' posts become unreadable.
Respect your tutors, respect yourself and respect the rules of this forum.
Happy learning !
Answer by Alan3354(69443)   (Show Source): (Show Source):
|
|
|
| |