|
Question 1142438: The high school is selling tickets for their upcoming concert and play. The tickets are $8 for adults and $6 for children. Alicia sells 24 tickets for $180. How many adult tickets and children’s tickets did she sell?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52754)   (Show Source):
You can put this solution on YOUR website! .
Let x be the number of adult tickets.
Then the number of children tickets is (24-x).
The "money" equation is
8x + 6*(24 - x) = 180 dollars.
From the equation, express "x" and calculate
x = 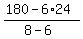 = 18.
ANSWER. 18 adult tickets and the rest 24-18 = 6 are the children tickets.
CHECK. 8*18 + 6*6 = 180 dollars. ! Correct !
Solved.
------------------
It is a standard ticket problem.
Read the lessons
- Using systems of equations to solve problems on tickets
- Three methods for solving standard (typical) problems on tickets
in this site.
From these lessons, learn on how to solve such problems once for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13195)  (Show Source):
You can put this solution on YOUR website!
This is, in essence, a mixture problem. You are mixing tickets at $6 each and tickets at $8 each to get tickets averaging some price in between.
Here is a solution method without algebra which, if you understand it, will get you to the answer to mixture problems like this much faster than the usual algebraic method.
(1) The average ticket price in this example is $180/24 = $7.50.
(2) Use any of a number of different methods to determine that $7.50 is 3/4 of the way from $6 to $8. (perhaps picture the three numbers on a number line...?)
(3) That means 3/4 of the tickets must be the more expensive $8 tickets.
ANSWER: 3/4 of the 24 tickets, or 18 tickets, were adult tickets; the other 1/4, or 6 tickets, were children's tickets.
|
|
|
| |
