|
Question 1142403: Find the equation of the line containing the points (4, -2) and (1, 3).
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! Find the equation of the line containing the points (4,-2) and (1,3).
-------
Don't put a space after the comma.
---
It's not "the equation" it's an equation.
---
There's more than 1 way to find them.
=============
Find the slope, m
m = diffy/diffx = 5/-3 = -5/3
Then, x-x1 = m*(y-y1) where (x1,y1 is either point.
---
x-1 = (-5/3)*(y-3)
That's an equation.
1-x = (5y/3) - 5
That's an equation.
---------------
|x y 1|
|4 -2 1| = 0
|1 3 1|
========
x*(-2*1 - 3*1) - y*(4*1 - 1*1) + 1*(4*3 - 1*-2) = 0
-5x - 3y + 14 = 0
---
That's an equation.
=====================
You can check for mistakes.
Sub for x & y in each equation.
Answer by ikleyn(52787)  (Show Source):
You can put this solution on YOUR website! .
First, calculate the slope.
The formula for the slope of a straight line passing through two given points ( , ) and ( , ) is
m =  .
Substitute the given data = 4, = -2, = 1, = 3 into the basic formula
m =  =  =  .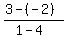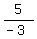
Next, write an equation of the line having the slope and passing through the given point (4,-2).
An equation of a straight line in a coordinate plane which has the slope m and passes through the given point P = (a,b) is
y - b = m*(x-a).
Substitute here m = , a = 4, b = -2, and you will get
y - (-2) = 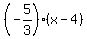 , or, equivalently,
y + 4 = .
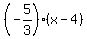Having the equation in this form, you can convert it to any other equivalent form you want.
----------------
See the lesson
- Equation for a straight line in a coordinate plane passing through two given points
in this site.
|
|
|
| |
