SOLUTION: For the experiment of rolling an ordinary pair of​ dice, find the probability that the sum will be less than 7 or greater than 11

There are 6 x 6 = 36 equally likely possible outcomes on the roll of two dice.

It is the total space of events.  Each event of the event space has the probability of  .


The sums less than 7 or greater than 11 are presented by this set of values {2, 3, 4, 5, 6, 12}.


There is  1 way  to get a 2:  (1,1).

There are 2 ways to get a 3:  (1,2) and (2,1).

There are 3 ways to get a 4:  (1,3), (2,2) and (3,1).

There are 4 ways to get a 5:  (1,4), (2,3), (3,2) and (4,1).

There are 5 ways to get a 6:  (1,5), (2,4), (3,3), (4,3) and (5,1).

There is  1 ways to get a 12: (6,6).


These pairs form the favorable set of events.


In all, there are 1+2+3+4+5+1 = 16 ways of occurring a sum less than 7 or greater than 11, so the probability under the question is


    P = 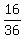 =  = 0.4444... = 44.44%  (approximately).


ANSWER.   P =  = 0.4444... = 44.44%  (approximately).