Question 1142381: The solutions of (2x − 5) / (3 − x) ≥ 0 are the values of x for which the graph of y = 2x^2 − 11x + 15
1. lies above the x - axis
2. lies on or above the x - axis, excluding x = 3
3. lies below the x - axis
4. lies on or below the x - axis, excluding x = 3
5. lies on or below the x - axis, excluding x = 3 and x = 5/2
Answer by greenestamps(13203)   (Show Source):
You can put this solution on YOUR website!
The critical points of the rational function 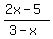 are the x values that make the numerator or denominator 0. Those values are x=5/2 and x=3. Note that x=5/2 is valid because 0 in the numerator is okay; x=3 is not valid because 0 in the denominator is not valid.
The zeroes of  are also x=5/2 and x=3.
The critical values of both functions divide the number line into 3 intervals: (-infinity,2.5), (2.5,3), and (3,infinity).
(1) Determine on which interval(s) the rational function is greater than or equal to 0, paying attention to whether the endpoints of each interval are included.
(2) For those intervals, determine whether the graph of 2x^2-11x+15 is above or below the x-axis.
(3) Select the correct answer choice.
|
|
|
