Question 1142347: One end of a spring is attached to the ceiling, and the other end of the spring is attached to a weight. The weight is pulled down (stretching the spring) and then released. The distance (in inches) between the weight and the ceiling after the weight is released, is given by the function. F(t)=6cos((2pie/3)t)+10
a). How far us the weight from the ceiling at he moment it is released?
b). How close does the weight get to the ceiling at its closet?
c). When is the first time that the weight is 13 inches from the ceiling?
d). List all of the times during the first 6 seconds after the weight is released that it is 13 inches from the ceiling.
Answer by ikleyn(52752)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The function is F(t) = 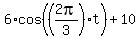 . .
The given function describes periodic oscillations of the mass around its averaged position at 10 inches from the ceiling
with the amplitude of 6 inches and the period of 3 seconds.
(a) At the moment t= 0, when the mass was released, its distance from the ceiling was 6 + 10 = 16 inches. ANSWER
(b) At its closest position from the ceiling, the distance of the mass from the ceiling is 10 - 6 = 4 inches. ANSWER
(c) First time the weight will be at 13 inches from the ceiling at the time moment t, when
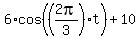 = 13, or = 13, or
 = 13 - 10 = 3, or = 13 - 10 = 3, or
 = =  = =  .
It means that at this moment .
It means that at this moment
 = =  ;
hence,
t = ;
hence,
t =  of a second. ANSWER
(d) The other time moments t <= 6 seconds, when the mass will be at the distance of 13 inches from the ceiling
are the OTHER solutions of the equation of a second. ANSWER
(d) The other time moments t <= 6 seconds, when the mass will be at the distance of 13 inches from the ceiling
are the OTHER solutions of the equation
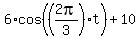 = 13, or = 13, or
 = 13 - 10 = 3, or = 13 - 10 = 3, or
 = =  = =  .
So, they are
t = 3 - .
So, they are
t = 3 -  = 2.5 seconds;
t = 3 + = 2.5 seconds;
t = 3 +  = 3.5 seconds, and
t = 6 - = 3.5 seconds, and
t = 6 -  = 5.5 seconds. = 5.5 seconds.
All questions are answered -- the problem is solved.
|
|
|