|
Question 1142065: Find the equation of the circle with center in the first quadrant, with radius 2 and tangent to the y-axis at (0,1).
Found 2 solutions by Theo, josmiceli:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the general form of the equation for a circle is (x-h)^2 + (y-k)^2 = r^2
(h,k) is the center of the circle.
r is the radius of the circle.
the radius is 2, so the formula becomes (x-h)^2 + (y-k)^2 = 4
the y-axis is tangent to the circle at (0,1).
since the tangent point is on the circle, then the opposite point from that, going through the center of the circle, would be (4,1).
that's because the radius of the circle is perpendicular to the tangent to the circle at the point of tangency.
the diameter of the circles is extend to the other side of the circle, with the length of the diameter being equal to 2 times the length of the radius.
that makes the length of the diameter equal to 4.
the center of the circle if half the distance of the diameter.
the diameter extends from (0,1) to (4,1) in a direction that is parallel to the x-axis and perpendicular to the y-axis.
the center of the circle is halfway between the points (0,1) and (4,1).
that places it at (2,1).
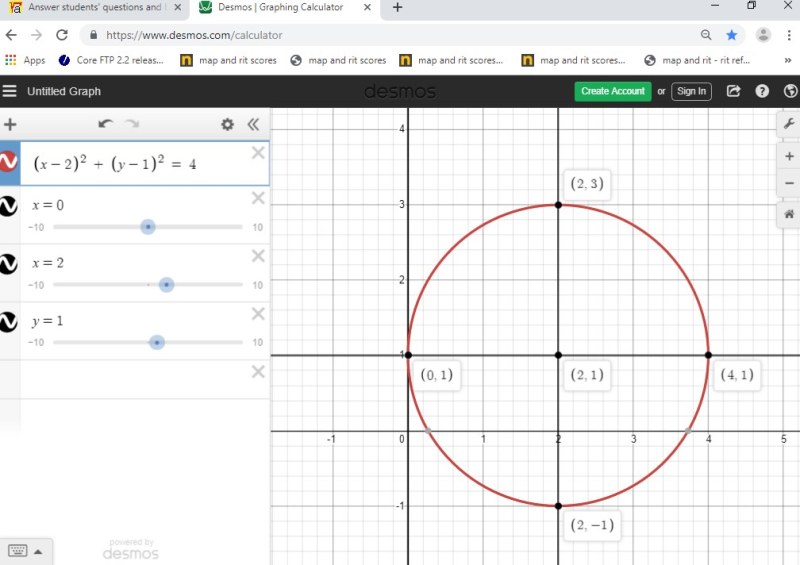
the equation of the circle becomes (x-2)^2 + (y-1)^2 = 4
the graph of that equation looks like this.
Answer by josmiceli(19441)   (Show Source): (Show Source):
|
|
|
| |