.
 = 1 - 2 = -1 ====>
= 1 - 2 = -1 ====>
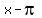 =
= 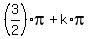 , where k is any integer . . . ====>
x =
, where k is any integer . . . ====>
x = 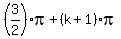 , where k is any integer . . .
And now my task is to choose "k" in a way to provide x =
, where k is any integer . . .
And now my task is to choose "k" in a way to provide x = 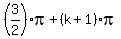 in the interval [
in the interval [ ,
, ).
For it, take k = -2; you will get x =
).
For it, take k = -2; you will get x = 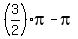 =
=  .
ANSWER. The solution is x =
.
ANSWER. The solution is x =  .
This solution is unique.
.
This solution is unique.
Solved.