Question 1141773: Given P(A)=0.24, P(B)=0.71, and P(A∩B)=0.13, what is P(B∣∣A^c)?
Answer by ikleyn(52847)   (Show Source):
You can put this solution on YOUR website! .
Given P(A)=0.24, P(B)=0.71, and P(A∩B)=0.13, what is P(B∣∣A^c)?
~~~~~~~~~~~~~~~~~
Looking into the post, I think that the symbol "||" (two vertical lines) is a typo, and it should be
only one vertical line instead of twos:
Given P(A)=0.24, P(B)=0.71, and P(A∩B)=0.13, what is P(B | A^c)?
I will solve the problem in this corrected formulation.
Solution
Use the basic formula (the definition) for the conditional probability
P(B | A^c) = P(B ∩ A^c) / P(A^c).
We have P(A^c) = 1 - P(A) = 1 - 0.24 = 0.76.
The set (B ∩ A^c) is part of B which does not belong to A, so
(B ∩ A^c) = B \ (A ∩ B); therefore, P(B ∩ A^c) = P(B) - P(A ∩ B) = 0.71 - 0.13 = 0.58.
Thus P(B | A^c) = P(B ∩ A^c) / P(A^c) = 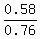 = 0.7632 (approximately). ANSWER
Completed and solved.
|
|
|
