Question 1141756: Matt and Anna Killian are frequent fliers on Fast-n-Go Airlines. They often fly between two cities that are a distance of 1980 miles apart. On one particular trip, they flew into the wind and the trip took 5.5 hours. The return trip with the wind behind them, only took about 4.5 hours. Find the speed of the wind and the speed of the plane in still air.
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52835)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Flying with the wind, their effective speed (the ground speed) was
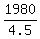 = 440 miles per hour.
This effective speed is the sum of the airplane speed "u" and the wind speed "v":
u + v = 440. (1)
Flying against the wind, their effective speed (the ground speed) was = 440 miles per hour.
This effective speed is the sum of the airplane speed "u" and the wind speed "v":
u + v = 440. (1)
Flying against the wind, their effective speed (the ground speed) was
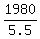 = 360 miles per hour.
This effective speed is the DIFFERENCE of the airplane speed "u" and the wind speed "v":
u - v = 360. (2)
Thus you have two equations (1) and (2) to determine two unknowns, u and v.
Add the equations (1) and (2), and you will get
2u = 440 + 360 = 800 ====> u = 800/2 = 400 mph.
It is the airplane speed at no wind.
Next, substitute the found value of "u" into equation (1) to find "v"
400 + v = 440 ====> v = 440 - 400 = 40 mph.
ANSWER. The airplane speed at no wind is 400 mph. The wind speed is 40 mph. = 360 miles per hour.
This effective speed is the DIFFERENCE of the airplane speed "u" and the wind speed "v":
u - v = 360. (2)
Thus you have two equations (1) and (2) to determine two unknowns, u and v.
Add the equations (1) and (2), and you will get
2u = 440 + 360 = 800 ====> u = 800/2 = 400 mph.
It is the airplane speed at no wind.
Next, substitute the found value of "u" into equation (1) to find "v"
400 + v = 440 ====> v = 440 - 400 = 40 mph.
ANSWER. The airplane speed at no wind is 400 mph. The wind speed is 40 mph.
-----------------
It is a typical "tailwind and headwind" word problem.
See the lessons
- Wind and Current problems
- Wind and Current problems solvable by quadratic equations
- Selected problems from the archive on a plane flying with and against the wind
in this site, where you will find other similar solved problems with detailed explanations.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the section "Word problems", the topic "Travel and Distance problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! going with the wind, the equation is (r + w) * t = d
going against the wind, the equation is (r - w) * t = d
r is the rate of the plane.
w is the rate of the wind.
t is the time.
d is the distance.
d is equal to 1980.
going with the wind, t = 4.5 hours.
going against the wind, t = 5.5 hours.
the equations become:
(r + w) * 4.5 = 1980
(r - w) * 5.5 = 1980
simplify to get:
4.5 * r + 4.5 * w = 1980
5.5 * r - 5.5 * w = 1980
multiply both sides of the first equation by (5.5 / 4.5) and leave the second equation as is to get:
5.5 * r + 5.5 * w = 2420
5.5 * r - 5.5 * w = 1980
subtract the second equation from the first to get:
11 * w = 440
solve for w to get w = 40.
replace w with 40 in the first original equation to get:
(r + w) * 4.5 = 1980 becomes (r + 40) * 4.5 = 1980
simplify to get 4.5 * r + 180 = 1980
subtract 180 from both sides to get 4.5 * r = 1980 - 180
combine like terms to get 4.5 * r - 1800
solve for r to get r = 400.
you have the rate (speed) of the plane = 400 miles per hour and the rate (speed) of the wind = 40 miles per hour.
going with the wind, the combined rate is 440 miles per hour * 4.5 hours = 1980 miles.
going against the wind, the combined rate is 360 miles per hour * 5.5 hours = 1980.
the numbers look good.
your solution is that the speed of the plane is 400 miles per hour and the speed of the wind is 40 miles per hour (rate and speed mean the same thing in this problem).
|
|
|