Question 1141667: The vertices of a triangle ABC A(2,4) B(-2,0) and C(6,-1).
(a) Find the coordinate of the midpoint P, Q, R of the sides AB, BC and CA respectively.
(b) Find the equation of the medians AQ and BR, and the coordinates of the point were they intersect.
(c) Show that the third median CP also passes through this point
Answer by MathLover1(20849)   (Show Source):
You can put this solution on YOUR website!
given:
The vertices of a triangle ABC
A( , )
B( , )
C( , )
(a) Find the coordinate of the midpoint P, Q, R of the sides AB, BC and CA respectively.
The midpoint of two points, ( ,  ) and ( ,  ) is the point M found by the following formula:
M= ( , )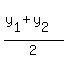
the coordinates of the midpoint P, of the sides AB are:
P = ( , )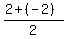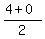
P = ( , )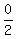
P = (,)
the coordinates of the midpoint Q, of the sides BC are:
Q=( , )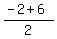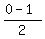
Q=(, )
the coordinates of the midpoint R, of the sides CA are:
R= ( , )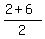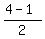
R= (, )
(b) Find the equation of the medians AQ and BR, and the coordinates of the point were they intersect.
the equation of the medians:
AQ =>
first use points A(,) and Q=(,) to find a slope
 => slope is undefined, and an undefined slope indicates that we have a vertical line parallel to the y-axis and passing through all points in the plane with an x-coordinate = constant ( c)
since both points  and  have same x-coordinate, the equation of the median is
and BR
B(,)
R= (,)
 ....simplify
now use point slope formula:
 ......plug in a slope and the coordinates of one point
now find the coordinates of the point were they intersect:
........eq.1
.......eq.2
------------------------------------
so, the coordinates of the point were they intersect is I=(, )
(c) Show that the third median CP also passes through this point
the third median CP:
C(,)
P = (,)
first find the equation of the median:
......plug in a slope and the coordinates of one point
plug in coordinates I=(,)
 => which is true and confirms that the third median CP also passes through the point I=(,)
|
|
|
