|
Question 114162: Identify a, b, and c after arranging the equation in standard form: 2x - x^2
Answer by bucky(2189)   (Show Source):
You can put this solution on YOUR website! The standard form for a quadratic equation is:
.
.
and in general, you are looking for the values of x where the graph crosses or just touches
the x-axis (presuming there is a real number solution to the problem). To find out if there
is a real solution, you set y equal to zero, making the standard form:
.
.
Back to your problem. You are told to arrange 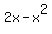 into the standard form. First write the  term and follow that by the  term to get:
.
.
Now compare this term by term with the corresponding terms in the standard forms listed previously.
Note that  compares with  . For these two terms to be identical,
a must be -1. Next, note that  compares with 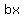 so that for these two terms
to be identical, b must be +2. Finally note that there is no constant in the function you
were given in the problem. Therefore, c must disappear in the standard form, and so c must be
zero.
.
So, your answer is a = -1, b = +2, and c = 0.
.
Hope this helps you to understand the problem.
.
|
|
|
| |
