Question 1141604: Paula, Cindy, and 10 of their friends have dinner at a round table with 12 chairs. The chairs are labeled 1 through 12. In how many ways can all 12 of them choose seats if Cindy sits to the left of Paula?
I have tried (11!/(0!11!));(11!/(10!11!)); and 10!
Found 2 solutions by josmiceli, greenestamps:
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! Paula and Cindy can sit In seats:
1,2
2,3
3,4
4,5
5,6
6,7
7,8
8,9
9,10
10,11
11,12
12,1
There are 12 different ways they can sit
since the seats are numbered
( but they can't swap places )
-----------------------------------
There are 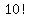 ways the other 10 ways the other 10
can be seated for each of the 12 ways, so


get a 2nd opinion if needed
Answer by greenestamps(13208)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I am suspicious about the wording of the problem. I'll come back to that later.
Since Cindy has to sit to the left of Paula, we can consider them as a single group; now the question is how many ways can we seat the 11 "people" (10 individuals and the Cindy-Paula pair) around the table.
Let's look at the general problem using smaller numbers.
The number of ways of seating 4 people in 4 seats in a row is 4! = 24. 4 choices for the person in the first seat, then 3 choices for the person in the 2nd seat, and so on.
The number of ways of seating 4 people around a circular table is not 4!, but 3!. That is because if the seats are in a row the arrangements ABCD and BCDA are different; but around a table they are indistinguishable. For any given ordering of the 4 people, there are 4 different "starting points"; so the number of different arrangements is 4!/4 = 3!.
So in this problem we have 11 objects around a table; the number of ways of arranging them is 10!.
That would be the answer to the usual problem like this.
However, in this problem, we are told the seats are numbered 1 through 12. That can be interpreted as meaning we don't have the problem of many different starting points for each sequence of people. If that is the meaning of that statement, then we have 12 different starting points for each of the 10! sequences of people; the number of arrangements is 12*10!.
... which agrees with the response from the other tutor....
|
|
|