please help me to find the equation of the graph which meets the x-axis at
-4 and 2,
Something was left out because there are infinitely many different
equations of graphs which meets the x-axis at -4 and 2. The easiest one is
y = (x+4)(x-2), which when multiplied out becomes
y = x²+2x-8 which has the graph:
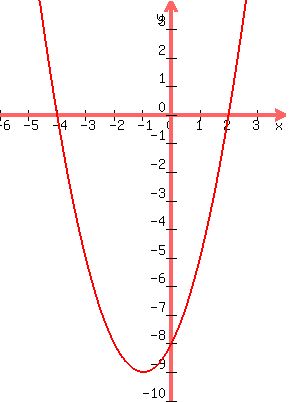
that part a) and part b)the coordinates of the turning point.
The turning-point of the graph of 
is the point
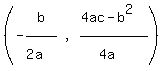For y = x²+2x-8, a=1. b=2, c=-8
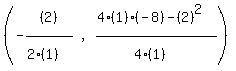which works out to be (-1,-9)
------------------------
Question two, the sketch of the graph y= 2+ 2x -x^2
passing through points E and G, a) find the coordinates of E and G.
Again, something was left out, because there is no way we can know what
points
E and G are.
b) find the maximum value of y. Thanking you in advance.
The maximum value of a quadratic graph that opens downward and the minimum
value of one that opens upward is the y-coordinate of the turning point.
The turning-point of the graph of is the point
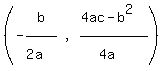Its y-coordinate 
. To determine a, b, and c, we
rewrite y= 2+2x-x² in its standard order
y = -x²+2x+2, so a=-1, b=2, c=2
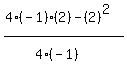That works out to be maximum of 3, and you can see that the turning point
is the highest point, and it is even with 3 on the y-axis.
Edwin
