Question 1141483: Four years ago a man was 2 and a 1/2 times as old as his son, but in five years time, he will only be twice as old as his son. How old is the man now?
Found 3 solutions by josgarithmetic, MathTherapy, ikleyn:
Answer by josgarithmetic(39615)   (Show Source):
Answer by MathTherapy(10550)  (Show Source):
You can put this solution on YOUR website!
Four years ago a man was 2 and a 1/2 times as old as his son, but in five years time, he will only be twice as old as his son. How old is the man now?
FYI: The man is NOT 85  years-old as reported by the other person.
Answer by ikleyn(52767)  (Show Source):
You can put this solution on YOUR website! .
Let y be the man's age, and
let n be the son's age.
From the condition, you have these two equations
y-4 = 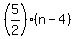 , (1)
y+5 = 2(n+5). (2)
Simplify, by multiplying equation (1) by 2 (both sides)'
2y-8 = 5n-20, (1')
y+5 = 2n+10 (2')
2y-5n = -12, (3)
y-2n = 5. (4)
Multiply equation (3) by 2;
Multiply equation (4) by 5.
4y-10n = -24, (5)
5y-10n = 25 (6)
Subtract equation (5) from equation (6). You will get
5y - 4y = 25 - (-24)
y = 49
ANSWER. The man's age is 49 years.
CHECK. Then from equation(2), 49+5 = 2*(n+5) ====> 54 = 2*(n+5) ====> n+5 = 54/2 = 27 ====> n = 27-5 = 22.
Thus the son's age is 22 years, and you can check that the equation (1) is valid, too. The check is completed.
|
|
|
