Question 1141476: Please help me solve this
Use the Binomial Theorem to expand (x-3y)^5
Found 2 solutions by greenestamps, MathLover1:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The binomial theorem looks scary to most students when they first see it. But with a little experience it is fairly easy to use -- especially if you understand WHY it works.
So let me start you on this with a demonstration; then you can finish.
The expression means you have five identical factors of (x-3y). When you expand the expression, you are going to get terms of x^5, x^4y, x^3y^2, x^2y^3, xy^4, and y^5.
Think about how many ways you are going to get each of those kinds of terms.
(1) x^5...
To get an x^5 term, you clearly need to choose the "x" term from all 5 factors (and the "-3y" term in 0 of them). The number of ways you can choose the "x" term in all 5 of the 5 factors is "5 choose 5" = C(5,5) = 1.
So the x^5 term will be  . .
(2) x^4y...
To get an x^4y term, you need to choose the "x" term from 4 of the 5 factors and the "-3y" term in 1 of them. The number of ways you can choose the x term in 4 of the 5 factors is "5 choose 4" = C(5,4) = 5.
So the x^4y term will be  . .
(3) x^3y^2...
To get an x^3y^2 term, you need to choose the "x" term from 3 of the 5 factors and the "-3y" term in 2 of them. The number of ways you can choose the x term in 3 of the 5 factors is "5 choose 3" = C(5,3) = 10.
So the x^3y^2 term will be  . .
I'll let you fill in the calculations to finish the expansion. The remaining terms are
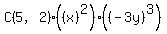

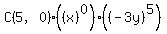
Answer by MathLover1(20850)   (Show Source): (Show Source):
|
|
|