Question 114138: The perimeter of a rectangle is 28 and its diagonal is 10. Find its length and width.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let L represent the length of the rectangle and W represent the width.
.
Since the perimeter (P) of a rectangle is the distance around it, the perimeter can be
written in equation form as:
.
P = L + W + L + W
.
and when like terms are combined, this simplifies to:
.
P = 2L + 2W
.
You are told that the perimeter is 28, so you can substitute 28 for P to make the equation:
.
28 = 2L + 2W
.
Next notice that when you draw a diagonal of the rectangle, the diagonal divides the rectangle
into 2 right triangles. Each of these triangles has as one of its legs L and as the other
leg W, and it has as its hypotenuse (longest side) the diagonal (D). Since both triangles
are right triangles, the Pythagorean theorem applies ... that is the sum of the squares of
the legs of one of these triangles equals the square of the hypotenuse. And since the
legs of one of the triangle are L and W and the hypotenuse is D, we can write the Pythagorean
equation as:
.

.
But the problem tells us that the diagonal, D, equals 10. Therefore 
and we can substitute that value into the Pythagorean equation in place of 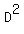 to to
get:
.

.
Now let's return to the perimeter equation and solve it for one of the variables in terms of
the other. The perimeter equation is:
.
28 = 2L + 2W
.
Divide both sides (all terms) by the common factor of 2 and you reduce this equation to:
.
14 = L + W
.
Let's subtract L from both sides to get rid of it on the right side and we get:
.
14 - L = W
.
Now we can substitute 14 - L for W in the Pythagorean equation because 14 - L and W are equals.
.
Begin with the Pythagorean equation:
.

.
and replace W with 14 - L to get:
.

.
Square out the expression in the parentheses and this equation becomes:
.

.
On the left side, combine the squared terms and arrange the terms in descending powers of L
to get:
.

.
Just to make things a little easier, note that 2 is a common factor of all terms, so
we can divide this entire equation (all terms) by 2 to get:
.

.
To get this into the more conventional form, get rid of the 50 on the right side by subtracting
50 from both sides to reduce the equation to:
.

.
Notice that the left side of this equation can be factored into:
.

.
and that this equation will be true if either of the two factors on the left side equals
zero ... because multiplication by zero on the left side will make the left side equal to
the zero on the right side.
.
So either  or or  If we solve these two equations for L, we find If we solve these two equations for L, we find
that either L = 8 or L = 6.
.
If L = 8, then we can go to the perimeter equation of  an substitute an substitute
8 for L to get:
.
14 = 8 + W
.
Subtracting 8 from both sides results in W = 6.
.
But if L = 6 and we go to the same perimeter equation, when we substitute 6 for L we get:
.
14 = 6 + W
.
and subtracting 6 from both sides we get W = 8. But this can't be because by definition
the width (W) is shorter than the length and in this case the width is 8 and the length is 6.
.
So the valid solution is the one in which we found the length is 8 and the width is 6.
.
Just as a check we can add 8 + 6 + 8 + 6 and find that the perimeter is 28, as the problem
said it should be. And we can apply the Pythagorean theorem:
.

.
and squaring the terms on the left side results in:
.

.
This simplifies to:
.

.
and taking the square root of both sides:
.

.
So when L = 8 and W = 6, the diagonal is 10, just as the problem said it is.
.
Our answer checks out.
.
Hope this helps you to understand the problem and one method by which the answer can be found.
.
|
|
|