Question 1141321: The half-life of carbon 14 is 5730 years. How old is a bone containing 20% of its original carbon 14?
Found 3 solutions by Boreal, Theo, josgarithmetic:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! P=Poe^-kt
when P/Po=0.5,
then 0.5=e^-kt
ln(0.5)=-k(5730)
-0.693=-5730k
k=+0.0001209
Let P=0.20Po
so P/Po=0.20
ln(0.20)=-0.0001209t=-1.609
so t=-1.609/-0.0001209
=13,308.52 years or 13309 years
If rounding only at end, it will be 13308 years.
This is between 2 and 3 half-lives, which is where 20% is.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the formula for continuous compounding is f = p * e ^ (r * t).
this is the formula that's most often used for determining growth rate of natural events.
if the growth rate is positive, then you are dealing with growth.
if the growth rate is negative, then you are dealing with decay.
f is the future value
p is the present value
r is the growth rate per time period.
t is the number of time periods.
the time period in this problem is in years.
if you assume the present value is 1, then the half life will be .5.
if the half life of carbon 14 is 5730 years, then your formula becomes:
.5 = 1 * e ^ (r * 5730)
this can be simplified to .5 = e ^ (r * 5730)
take the natural log of both sides of this equation to get ln(.5) = ln(e ^ (r * 5730)).
since ln(e ^ (r * 5730) = r * 5730 * ln(e), and since ln(e) = 1, then your equation becomes:
ln(.5) = r * 5730
divide both sides of this equation by 5730 to get ln(.5) / 5730 = r
solve for r to get r = -1.20968094 * 10 ^ -4).
that equivalent to r = -.000120968094.
confirm by replacing r in the original equation with that to get .5 = e ^ (r * 5730) becomes .5 = e ^ (-.000120968094 * 5730) which becomes .5 = .5, confirming the solution is correct.
you now know the value of r and you want to know how long it will take to have 20% of the original carbon 14 still in the bones.
the same equation is used, only this time you know the value of r but don't know the value of t.
the future value becomes .2.
the formula becomes .2 = 1 * e ^ (-.000120968094 * t)
this simplifies to .2 = e ^ (-.000120968094 * t)
take the natural log of both sides of this equation to get ln(.2) = ln(e ^ (-.000120968094 * t)).
since ln(e ^ (-.000120968094 * t)) is equal to -.000120968094 * t * ln(e), and since ln(e) = 1,then your equation becomes:
ln(.2) = -.000120968094 * t.
divide both sides of this equation by -.000120968094 to get ln(.2) / -.000120968094 = t.
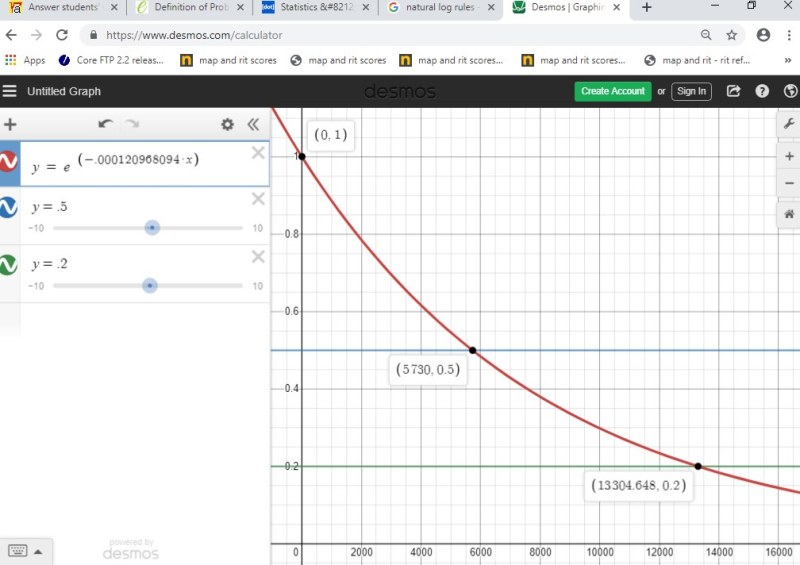
solve for t to get t = 13304.64798.
the amount of carbon 14 in the bones will be 20% in 13304.64798 years.
confirm by replacing t with 13304.64798 in the original equation to get:
.2 = e ^ (-.000120968094 * t) becomes .2 = e ^ (-.000120968094 * 13304.64798) which becomes .2 = .2, confirming the solution is correct.
the formula can be graphed as y = e^(-.000120968094 * x).
here's what it looks like.
Answer by josgarithmetic(39625)   (Show Source): (Show Source):
|
|
|