SOLUTION: A five digit number is formed using digits 0 1 2 3 and 4 without repetition. Find the chance that the number is divisible by 5.

Click here to see ALL problems on Probability-and-statistics

Question 1141202: A five digit number is formed using digits 0 1 2 3 and 4 without repetition. Find the chance that the number is divisible by 5.
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443) (Show Source):
You can put this solution on YOUR website!
A five digit number is formed using digits 0 1 2 3 and 4 without repetition. Find the chance that the number is divisible by 5.
----------------
The units digit has to be 5 or zero to be divisible by 5. There's no 5, so it has to be zero.
---> 1 out of 5
============
Not sure about "the chance."
Probability is 1/5
Odds are 1:4

Answer by ikleyn(52786) (Show Source):
You can put this solution on YOUR website!
.

First, let us calculate the number of all possible five digit numbers formed using the digits 0, 1, 2, 3 and 4 without repetition. The leftmost digit can be any of four digits 1, 2, 3 or 4, which gives 4 options. The next digit can be any of 4 remaining digits, which gives 4 options. Using similar arguments, you will get 4*4*3*2*1 = 96 for the number of all possible five digit numbers formed using the digits 0, 1, 2, 3 and 4 without repetition. The numbers divisible by 10 are those of them that ended by 0 (by zero), and the number of such numbers is 4*3*2*1 = 24. Thus the probability P under the question is the ratio P = 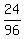= = 0.25 = 25%. ANSWER