Question 1141044: The coordinates of 3 points are A(1,5), B(9,7) and C(k,-6).
M is the midpoint of AB and MC is perpendicular to AB.
Find the value of k.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! given:
The coordinates of 3 points are A( , , ), B( ), B( , , ) and C( ) and C( , , ). ).
 is the midpoint of is the midpoint of  and and 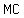 is perpendicular to is perpendicular to  . .
Find the value of  . .
first find equation of the line that passes through  and and  : :
 ........use A( ........use A( , , ), B( ), B( , , ) to find a slope ) to find a slope 

 ......use one point to find ......use one point to find 



equation is: 
now, if  is the is the 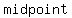 of of  , coordinates of the midpoint , coordinates of the midpoint are: are:
( , , )=( )=( , , ) )
if 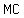 is perpendicular to is perpendicular to  , find the equation of the line perpendicular to , find the equation of the line perpendicular to  that passes through point that passes through point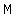
a slope of the line perpendicular to  is negative reciprocal to is negative reciprocal to  , and it is , and it is

so,  .....use the point .....use the point  to find to find 




equation the line perpendicular to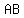 is: is:
 ......use the point C( ......use the point C( , , ) to find ) to find 





so, C( , , ) )

|
|
|