Question 1141003: Find three consecutive odd integers such that the sum of two times the first, three times the second, and one time the third is 412. List the numbers in order from smallest to largest.
Found 2 solutions by ikleyn, 4419875:
Answer by ikleyn(52898)   (Show Source):
You can put this solution on YOUR website! .
Let n be the smallest of the three consecutive odd integer numbers.
Then the three numbers are n, (n+2) and (n+4).
The equation is
2n + 3*(n+2) + (n+4) = 412
2n + 3n + 6 + n + 4 = 412
6n + 10 = 412
6n = 412 - 10
6n = 402
n = 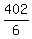 = 67.
ANSWER. The three numbers are 67, 69 and 71.
Answer by 4419875(21)  (Show Source):
You can put this solution on YOUR website! the orientation will be like this:
2(x+1)+3(x+3)+(x+5) = 412
where:
2 times the 1st -> 2(x+1)
3 times the 2nd -> 3(x+3)
1 times the 3rd -> (x+5)
Thus,
6x + 16 = 412
6x = 396
x = 66
so the numbers would be
[66+1, 66+3, 66+5]
[67, 69, 71]
to check if it's true
2(66+1)+3(66+3)+(66+5)= 412
134 + 207 + 71 = 412
412 = 412
Hope to do your homework well. Goodluck
|
|
|
