Question 1140609: a list of whole numbers from 1 to 50 is written on a piece of paper. all the multiples of 5 are then struck off from the list. what is the last digit of the product of the remaining numbers.
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! a list of whole numbers from 1 to 50 is written on a piece of paper. all the
multiples of 5 are then struck off from the list. what is the last digit of the
product of the remaining numbers.
There is an easy way and a hard way:
Here's the easy way:
The last digits of the whole numbers from 1 to 50 (inclusive) make up 5 groups
of 1,2,3,4,5,6,7,8,9,0. When we take away the multiples of 5, we take away
those ending in 0 or 5, and that leaves 5 groups of 1+2+3+4+6+7+8+9 = 40, and
adding any whole number of groups of 40 will end up having a 0 for the last
digit of the sum.
Answer: 0
Now for the hard way:
First we find the sum of 1+2+3+···+48+49+50
The formula for the sum of the first N whole numbers, since they form an
arithmetic sequence where a1 = 1, n=50, and an = a50 = 50
 becomes becomes


 Now from that we must subtract this sum: 5+10+15+···+40+45+50, which forms
an arithmetic sequence where a1 = 5. But how am I going to find out
what to substitute for n? This way:
If we divide every number in this series
5+10+15+···+40+45+50
by 5, we get this series:
1+2+3,···,8+9+10
and since we know that has 10 terms, so does the first one! So n=10,
and an = a10 = 50,
Now from that we must subtract this sum: 5+10+15+···+40+45+50, which forms
an arithmetic sequence where a1 = 5. But how am I going to find out
what to substitute for n? This way:
If we divide every number in this series
5+10+15+···+40+45+50
by 5, we get this series:
1+2+3,···,8+9+10
and since we know that has 10 terms, so does the first one! So n=10,
and an = a10 = 50,
 becomes becomes


 So to get the final answer the hard way, we subtract:
1275-275 = 1000, which ends in 0. <-- final answer
The easy way is better! J
I confess! I did it the hard way first, and then the easy way dawned on me and I felt stupid!
Edwin
So to get the final answer the hard way, we subtract:
1275-275 = 1000, which ends in 0. <-- final answer
The easy way is better! J
I confess! I did it the hard way first, and then the easy way dawned on me and I felt stupid!
Edwin
Answer by ikleyn(52831)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a list of whole numbers from 1 to 50 is written on a piece of paper. all the multiples of 5 are then struck
off from the list. what is the last digit of the product of the remaining numbers.
~~~~~~~~~~~~~~~~~~
Edwin solved totally different problem, irrelevant to the problem's question.
So I came to solve the real problem.
First 10 numbers of the sequence are
1 2 3 4 5 6 7 8 9 10
When you take off 5 and 10 from this list, you will get the sequence
1 2 3 4 6 7 8 9
The product of these numbers is 1*2*3*4*6*7*8*9 = 72576.
The last digit of this product is 6.
It gives you an idea that the last digit of the number under the question is 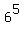 = 6. ANSWER = 6. ANSWER
|
|
|