Question 1140428: the first term of a geometric series is 3,the last term is 768 if the sum of the term is 1533 find the common ratio and the number of terms
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52803)   (Show Source):
You can put this solution on YOUR website! .
The formula for the sum of the first "n" terms of any geometric progression
 = 
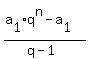(where "q" is the common ratio) can be written in an equivalent form
=  .
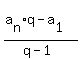So, with the given data,
1533 =  ,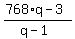
or, simplifying
768*q - 3 = 1533*(q-1)
768q - 3 = 1533q - 1533
1533 - 3 = 1533q - 768q
1530 = 765q
q = 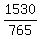 = 2.
So, the common ratio is just found: it is 2.
Next, to find "n", the number of terms, use the general formula for the n-th term
768 =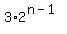 
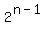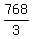 =  = 256
============> n - 1 = 8; hence, n = 9.
ANSWER. The number of terms is 9 and the common ratio is 2.
--------------
On geometric progressions, see introductory lessons
- Geometric progressions
- The proofs of the formulas for geometric progressions
- Problems on geometric progressions
- Word problems on geometric progressions
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic
"Geometric progressions".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
Answer by greenestamps(13200)  (Show Source):
|
|
|
