Question 1140355: In 2 1/2 hours an airplane travels 400 km against the wind. It takes 50 min to travel 200 km with the wind. Find the speed of the wind and the speed of the airplane in still air.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52786)   (Show Source):
You can put this solution on YOUR website! .
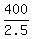 = 160 mph is the speed of the airplane against the wind, which is u - v,
where u is the speed of the airplane in still air, v is the speed of the wind.
So, one equation is
u - v = 160. (1)
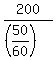 = 240 mph is the speed of the airplane with the wind, which is u + v.
So, the other equation is
u + v = 240. (2)
From equations (1) and (2) you get (using elimination or substitution method)
u = 200 mph; v = 40 mph. ANSWER
Solved.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The speed against the wind is 400/2.5 = 160km/hr; the speed with the wind is 200/(5/6) = 240km/hr.
The speed with the wind is the sum of the plane's speed and the wind speed; the speed against the wind is the difference between the plane's speed and the wind speed.
So this is one of a large number of different kinds of problem where you need to find two numbers if you know the sum of the two numbers and the difference between them.
Of course algebra is a good way to solve a problem like that. However, since this kind of problem is encountered frequently, you can save time and effort by learning to solve the problem quickly with logical reasoning.
You know the sum of the plane's speed and the wind speed is 240km/hr, and you know that the difference between the two speeds is 160km/hr. Logical reasoning (picture the numbers on a number line) tells you that the plane's speed is halfway between those two speeds; and then the wind speed is the difference between the plane's speed and each of those two speeds. So...
The plane's speed is halfway between 160km/hr and 240km/hr: 200 km/hr. And the wind speed is the difference between 200 and 240km/hr (or the difference between 200 and 160km/hr), which is 40km/hr.
ANSWER (by logical reasoning instead of formal algebra): Plane speed 200km/hr; wind speed 40km/hr.
|
|
|
