SOLUTION: 1. factorise x^4-5x^3+5x^2+5x-6 2. x^9-y^9 3. solve the equation x^4-5x^3+5x^2+5x-6=0 4. 7e^x - 3 = 2e^(2x)

1.   Factor:  

All potential roots or zeros are ± the factors of 6, which are ±1,±2,±3,±6

We try the easiest one first, which is 1 with synthetic division,  We are
dividing by x-1

1 | 1 -5  5  5 -6
  |    1 -4  1  6
    1 -4  1  6  0

Luckily that gave 0 remainder, telling us that 1 is a zero or root and that
x-1 is a factor,  So the first partial factorization using (x-1) and the bottom
numbers is:

(x-1)(x³-4x²+x+6)

Next we factor x³-4x²+x+6

All potential roots or zeros are again ± the factors of 6, which are ±1,±2,±3,±6

We try the easiest one first again, which is 1, with synthetic division,  We are
again dividing by x-1

1 | 1 -4  1  6
  |    1 -3 -2
    1 -3 -2  4

That does not give 0 remainder, so we try the next easiest one, which is -1,
with synthetic division,  We are dividing this time by x+1

-1 | 1 -4  1  6
   |   -1  5 -6
     1 -5  6  0

Luckily that gave 0 remainder, telling us that -1 is a zero or root and that
x+1 is a factor,  So the next partial factorization using (x+1) and the bottom
numbers is:

(x-1)(x+1)(x²-5x+6)

Now we can complete the factorization without synthetic division:

(x-1)(x+1)(x-2)(x-3)

------------------------------------------

Factor: 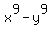 , we rewrite as  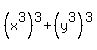and
then we can use the formula: 
with A=x³ and B=y³





-------------------------------------------

3.solve the equation 

We have already factored the left side in the first problem, so
we have:

(x-1)(x+1)(x-2)(x-3) = 0

We set each factor equal to 0:

x-1=0;  x+1=0;  x-2=0;  x-3=0
  x=1;    x=-1;   x=2;    x=3

Those are the four solutions.

----------------------------------

4.  

Let ex = u, then e2x = u2

    
    
    
    
    2u-1=0;   u-3=0
      2u=1      u=3
       u=

Substitute ex for u

;   
;  
;


Here ln() means natural logarithm.

Edwin