Question 1139968: Two buses are driving along parallel freeways that are 5𝑚𝑖 apart, one heading east and the other heading west. Assuming that each bus drives a constant 55𝑚𝑝ℎ, find the rate at which the distance between the buses is changing when they are 13𝑚𝑖 part, heading toward each other.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If we count time from the moment the buses are approaching each other but still 13 miles apart, the distance  (in miles) between the buses as a function of time (in miles) between the buses as a function of time  (in hours) is (in hours) is


As the buses are passing each other, their distance is about 5 miles, and not changing very sharply. When they are very far from each other their distance is changing by almost 110mph. At a time  , the rate of change (in mph) for the distance between the buses is the value of the derivative of the function , the rate of change (in mph) for the distance between the buses is the value of the derivative of the function 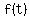 above. above.
That derivative, 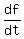 or or 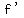 is the function is the function
 , and its value at , and its value at  is is
 . .
It is a negative value, because the distance is decreasing, and in absolute value is approximately 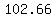 . .
When the buses are at 13 miles from each other, approaching each other, the distance between them is decreasing at  . .
|
|
|