Question 1139868: Find the sum of all even numbers from 4 to 100 inclusive, excluding those which are multiples of 3.
Found 3 solutions by MathLover1, ikleyn, MathTherapy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! the sum of all even numbers from  to to  inclusive, excluding those which are multiples of inclusive, excluding those which are multiples of  . .
We have to find the number of terms that are divisible by  but not by but not by  ( as the question asks for the even numbers only which are not divisible by ( as the question asks for the even numbers only which are not divisible by  ) )
For  , ,
 , , , , ,........., ,.........,
using AP formula, we can say 




For  , ,
 , , , , ,...... ,......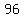
using AP formula, we can say 




 is the number of terms that are divisible by is the number of terms that are divisible by  but not by but not by 
here are they: all divisible by  , highlighted divisible by , highlighted divisible by 
 , ,  , ,  , ,  , ,  , ,  , ,  , , , ,  , ,  , ,  , , 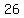 , , 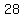 , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , , 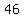 , ,  , , , ,  , ,  , ,  , ,  , , , ,  , ,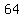 , , , ,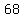 , ,  , , , , 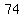 , ,  , ,  , ,  , ,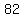 , ,  , ,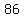 , ,  , ,  , ,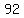 , ,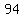 , ,  , , , ,
now add all 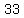 numbers that are not highlighted numbers that are not highlighted

Answer by ikleyn(52879)   (Show Source): (Show Source):
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the sum of all even numbers from 4 to 100 inclusive, excluding those which are multiples of 3.
Number of EVEN numbers, from 4 to 100, inclusive: 
Sum of the 49 EVEN numbers, from 4 to 100, inclusive: 
Number of EVEN numbers, from 4 to 100, inclusive, that're MULTIPLES of 6 (2 * 3): 
Sum of the 16 EVEN numbers, from 4 to 100, inclusive, that're MULTIPLES of 6: 
Sum of ALL EVEN numbers, from 4 to 100, inclusive, that're NOT MULTIPLES of 6: 
|
|
|