SOLUTION: The median life of Brand LT5 batteries is 100 hours. What is the probability that in a set of three such batteries, exactly two will last longer than 100 hours?

Algebra ->  Probability-and-statistics -> SOLUTION: The median life of Brand LT5 batteries is 100 hours. What is the probability that in a set of three such batteries, exactly two will last longer than 100 hours?      Log On


   

Question 1139701: The median life of Brand LT5 batteries is 100 hours. What is the probability that in a set of three such batteries, exactly two will last longer than 100 hours?
Answer by ikleyn(52844) About Me  (Show Source):
You can put this solution on YOUR website!
.

        I just saw  (and solved)  several similar problems in this forum.

        They are not exactly and precisely mathematical, since the condition is not completed and requires some additions.

        Again,  they are not exactly and precisely mathematical,  but mostly serve to exercise your  "common sense".

        They require you to reformulate the condition in a way the problem to obtain its sense.

        And they require such an addition 

           a)  "to be consistent"  with the given part,  and  

           b)  to be likelihood.


        So, again, it is not "the pure Mathematics in its pure instance" - it is the common sense hypothesizing
        to make right formulation and to get the problem solved     (  =   to get a likelihood solution ).

        After this introduction,  I can now move to the solution. 


Having nothing else given, an appropriate hypothesis is to assume that we have continuous random variable 


    X = "the time of a battery service / (or "life")" 


with random values that are uniformly distributed with the minimum value of 0 and the maximum value of 200 hours.


Then the mean average  is exactly 100, as the problem states, and  the condition becomes "consistent with the given part" and "self-closed".


Then the probability  P(X < 100) = 1%2F2, as well as  P(x > 100) = 1%2F2.


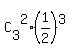Therefore, the probability that exactly two of the three batteries will last longer than 100 hours is  C%5B3%5D%5E2%2A%281%2F2%29%5E3 = 3%2F8.

Solved.

-----------------

See the lesson
    - Unusual probability problems
in this site,  where you will find many other similar problems solved and explained.


==============

WARNING ! : When I posted similar solution to a similar problem to one of the visitors of this forum,

he (or she) posted me back "the empty line response", expressing his (or her) dissatisfaction,

and I momentarily got understanding that this person is an idiot.

So, carrying about your reputation, please do not repeat this stupid action, because right now you got
a BRILLIANT SOLUTION with a BRILLIANT EXPLANATION.