Question 1139591: The cost C (in dollars) for a company to produce and sell x thousand gadgets is given by 
What is the minimum cost?
I've found that the start up cost is 2530 dollars.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I think you meant to say  instead of instead of 
The difference is that the  term is not in the denominator. term is not in the denominator.
To make sure you do not divide by  , you would write it like this , you would write it like this
C = (1/30)x^2 - 2x + 2530
If my assumption is correct, then we have an equation in the form

where
a = 1/30
b = -2
c = 2530
Use the 'a' and 'b' values to compute the value of h, which is the x coordinate of the vertex
h = -b/(2a)
h = -(-2)/(2*(1/30))
h = 2/(2/30)
h = (2/1) / (2/30)
h = (2/1) * (30/2)
h = (2*30)/(1*2)
h = 60/2
h = 30
The x coordinate of the vertex is 30.
The y coordinate of the vertex is k, which is defined as k = f(h)
For this problem, k = f(30)
In other words, we plug in x = 30 to find the y coordinate of the vertex.

 Replace every x with 30; use PEMDAS to simplify Replace every x with 30; use PEMDAS to simplify



We see that k = 2500, meaning the y coordinate of the vertex is 2500.
The vertex is at (h,k) = (30, 2500) which in this case is the lowest point of the parabola. The parabola has a lowest point any time 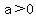 (in this case, a = 1/30 = 0.033 approximately) (in this case, a = 1/30 = 0.033 approximately)
The graph confirms the answer

The graph was created with GeoGebra (free graphing software). I used the "min" feature in GeoGebra to find/display point A as shown in the diagram above.
The vertex point (30, 2500) means that if you produce and sell 30 thousand gadgets, then the minimum cost is $2500
side note: keep in mind that x is in thousands. So x = 30 really means 30,000.
---------------------------------------------------------------------
Answer:
The minimum cost is 2500 dollars
|
|
|