SOLUTION: Solve the system of inequalities and indicate all the integers which are in the solution set: 2−6y<14 1<21−5y

You have this system


    2 - 6y < 14,       (1)

    1 < 21 - 5y.       (2)


By default, it means that you should find the solution set to each inequality SEPARATELY, 

and then take the common part of these two sets, i.e. the intersection of the separate solution sets.


OK. Let' start from the first inequality


1)    2 - 6y < 14  is equivalent to  2 - 14 < 6y,   -12 < 6y,   y >  = -2.


      Thus { y > -2 }  is the solution set to the first inequality.



Next, let's solve the second inequality



2)    1 < 21 - 5y  is equivalent to  5y < 21 - 1,   5y < 20,   y < 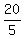 = 4.


      Thus { y < 4 }  is the solution set to the second inequality.



3)    Now, the solution to the given system is the common part of the two solution sets, 

      i.e. their intersection, which is the interval  (-2,4).



ANSWER.  The solution to the given system is the set  -2 < x < 4, or, which is the same, the interval (-2,4).


         The integers in this interval are -1, 0, 1, 2, 3.