Question 1139126: Find the lump sum that one must invest in an annuity in order to receive R1 000 at the end of each month for the next 16 years, if the annuity pays 9% per annum, compounded monthly.
Answer by ikleyn(52887)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The usual (the regular, the traditional) formulation of such problems considers withdrawing money
at the BEGINNING of each month (with the compounding still at the end of each month).
It is also coherent (consistent) with the common sense: you need money at the beginning of each month to spend them
during the month - not at the end of the month.
So, I will edit your formulation in this way
Find the lump sum that one must invest in an annuity in order to receive R 1000 at the  beginning of each month
for the next 16 years, if the annuity pays 9% per annum, compounded monthly. beginning of each month
for the next 16 years, if the annuity pays 9% per annum, compounded monthly.
Solution
For this problem, the general formula is
X =  .
where X is the lump sum to deposit at the account once at the beginning.
In this case, the withdrawal monthly rate is W = R 1000, the monthly compounding rate is r = 0.09/12 = 0.0075,
p = 1 + r = 1 + 0.0075 = 1.0075, the number of withdrawing periods is n = 16*12 = 192
(same as the number of compounding periods). So
X = .
where X is the lump sum to deposit at the account once at the beginning.
In this case, the withdrawal monthly rate is W = R 1000, the monthly compounding rate is r = 0.09/12 = 0.0075,
p = 1 + r = 1 + 0.0075 = 1.0075, the number of withdrawing periods is n = 16*12 = 192
(same as the number of compounding periods). So
X = 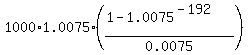 = 102334.56. ANSWER
ANSWER. The lump sum to deposit at the account once at the beginning is R 102334.56. = 102334.56. ANSWER
ANSWER. The lump sum to deposit at the account once at the beginning is R 102334.56.
Solved.
--------------
See my lessons in this site associated with annuity saving plans and retirement plans
- Ordinary Annuity saving plans and geometric progressions
- Annuity Due saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
- Withdrawing a certain amount of money periodically from a compounded saving account (*)
- Miscellaneous problems on retirement plans
in this site, and especially lesson marked (*) in the list as the most relevant to the given problem.
|
|
|