|
Question 1139088: Benjamin & Associates, a real estate developer, recently built 198 condominiums in McCall, Idaho. The condos were either three-bedroom units or four-bedroom units. If the total number of rooms in the entire complex is 710, how many three-bedroom units are there? How many four-bedroom units are there?
Answer by ikleyn(52898)   (Show Source):
You can put this solution on YOUR website! .
Let x = # of three-bedroom units, y = # of four-bedroom units.
From the condition, you have these 2 equations
x + y = 198 (1) (counting units)
3*x + 4*y = 710 (2) (counting rooms)
From equation (1), express y = 198 - x and substitute it into equation (2). You will get
3x + 4*(198-x) = 710.
Express x and calculate answer
x = 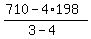 = 82.
Then from equation (1), y = 198 - 82 = 116.
ANSWER. 82 three-bedroom units and 116 four-bedroom units.
CHECK. 3*82 + 4*116 = 710 rooms. ! Correct !
The problem solved using 2-equation setup and the Substitution method.
--------------
It is a standard and typical ticket problem.
For ticket problems, read the lessons
- Using systems of equations to solve problems on tickets
- Three methods for solving standard (typical) problems on tickets
in this site.
From these lessons, learn on how to solve such problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
|
|
|
| |
