.
After 1-st transfer,
With the probability 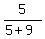 =
= 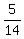 you will get (7+1 blue, 3 green) = (8 blue,3 green) in the bag
(call it "case A". It is the case when a blue jelly was transferred);
with the probability
you will get (7+1 blue, 3 green) = (8 blue,3 green) in the bag
(call it "case A". It is the case when a blue jelly was transferred);
with the probability 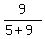 =
= 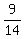 you will get (7 blue, 3+1 green) = (7 blue,4 green) in the bag
(call it "case B". It is the case when a green jelly was transferred).
After the selection from the bag,
the probability to get a green jelly from the bag is
you will get (7 blue, 3+1 green) = (7 blue,4 green) in the bag
(call it "case B". It is the case when a green jelly was transferred).
After the selection from the bag,
the probability to get a green jelly from the bag is  =
= 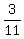 in case A, and
the probability to get a green jelly from the bag is
in case A, and
the probability to get a green jelly from the bag is 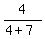 =
= 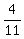 in case B.
Thus the probability to get a green jelly from the bag is
P(green) =
in case B.
Thus the probability to get a green jelly from the bag is
P(green) = 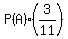 +
+ 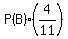 =
= 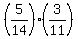 +
+ 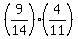 =
= 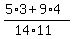 =
= 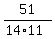 .
Now use the formula for conditional probability to get the answer to the problem's question
P(green at the first transfer) =
.
Now use the formula for conditional probability to get the answer to the problem's question
P(green at the first transfer) = 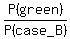 =
= 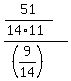 =
= 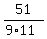 =
= 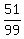 =
= 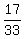 . ANSWER
. ANSWER
Completed and solved.