Is there any one that knows how to work this problem?
Find the zeros of f.
To find the zeros substitute 0 for f(x) and solve for x.

 Get 0 on the right:
Get 0 on the right:
 Factor out
Factor out 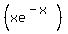
 Now we use the zero product principle.
There are three factors:
Now we use the zero product principle.
There are three factors:  ,
,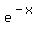 , and
, and  Setting x = 0 gives one solution, namely x = 0
Setting
Setting x = 0 gives one solution, namely x = 0
Setting 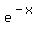 = 0 gives no solution, since
= 0 gives no solution, since 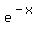 is never 0.
Setting x-2 = 0 gives a second solution, namely x = 2
So there are two zeros, 0 and 2.
Edwin
is never 0.
Setting x-2 = 0 gives a second solution, namely x = 2
So there are two zeros, 0 and 2.
Edwin