SOLUTION: Can anyone help me set up and solve this word problem? I am lost. Thank you in advance. During the first part of a​ trip, Adrian drove 21 miles at a certain speed. Adrian dr

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: Can anyone help me set up and solve this word problem? I am lost. Thank you in advance. During the first part of a​ trip, Adrian drove 21 miles at a certain speed. Adrian dr      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1138796: Can anyone help me set up and solve this word problem? I am lost. Thank you in advance.
During the first part of a​ trip, Adrian drove 21 miles at a certain speed. Adrian drives another 21 miles on the second part of the trip at a speed 10 mph faster. Driving time for the entire trip was 80 mins. Find the rate at which Adrian drove during the first part of the trip.
The rate at which Adrian drove during the first part of the trip is_______.
Answer by ikleyn(52879) About Me  (Show Source):
You can put this solution on YOUR website!
.
Let x be the rate on the first part of the trip, in miles per hour.

Then the rate on the second part was  (x+10) mph, according to the condition.


The time to travel the first part  was  21%2Fx  hours.

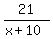The time to travel the second part was  21%2F%28x%2B10%29.


The total time is the sum of these partial times, which gives you the "time" equation


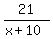    21%2Fx + 21%2F%28x%2B10%29 = 80%2F60,  or


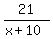    21%2Fx + 21%2F%28x%2B10%29 = 4%2F3  hours.


To solve the equation, multiply both sides by 3x*(x+10).  You will get


    63*(x+10) + 63*x = 4x*(x+10).


Simplify it step by step and solve 


    63x + 630 + 63x = 4x^2 + 40x

    4x^2 - 86x - 630 = 0

    2x^2 - 43x - 315 = 0


Solve this quadratic equation and take its positive root.
It will be your solution/answer.