Question 1138795: Please help me solve for x in
4logx to base 16 = log(x + 12) to base 4
Found 3 solutions by MathLover1, ikleyn, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The original equation is
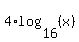 = = 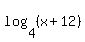 .
Note that the domain, where both sides are defined, is the set of positive real x: { x | x > 0 }.
Due to properties of logarithms, it is the same as .
Note that the domain, where both sides are defined, is the set of positive real x: { x | x > 0 }.
Due to properties of logarithms, it is the same as
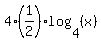 = = 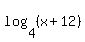 , or, equivalently, , or, equivalently,
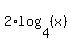 = = 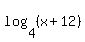 , which, in turn, is equivalent to , which, in turn, is equivalent to
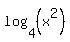 = = 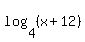 .
It implies
x^2 = x + 12
x^2 - x - 12 = 0,
(x-4)*(x+3) = 0.
Of the two roots, x= 4 and x= -3, only positive x= 4 is in the domain and is, therefore, the solution.
ANSWER. x= 4. .
It implies
x^2 = x + 12
x^2 - x - 12 = 0,
(x-4)*(x+3) = 0.
Of the two roots, x= 4 and x= -3, only positive x= 4 is in the domain and is, therefore, the solution.
ANSWER. x= 4.
Solved. // I mean, solved in a way as it should be done.
--------------
On the way, I used standard and elementary properties of logarithms that every student must learn and must know
before starting solving such problems.
On logarithms and their properties, see the lessons
- WHAT IS the logarithm
- Properties of the logarithm
- Change of Base Formula for logarithms
- Solving logarithmic equations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Logarithms".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There is certainly no need to get into 4th degree polynomial equations in solving this problem.
With only a little bit of experience, when you see an equation involving a log base 16 and a log base 4, you should recognize that almost certainly you will want to change the equation into an equation involving only base 4 logs or only base 16 logs.
In this problem, log of x base 16 is half as big as log base x of 4, because the base 16 is the square of the base 4. So the left side of the equation, 4 times log base 16 of x, converts to 2 times log base 4 of x, and the solution is far easier because you end up with a quadratic equation instead of a quartic.
So go the path shown by tutor @ikleyn....
|
|
|