SOLUTION: You have a plate of 45 cookies. Ten have chocolate chips and 15 have pecans. Of the cookies mentioned in the preceding sentence, 6 have both chocolate chips and pecans. You select

Algebra ->  Probability-and-statistics -> SOLUTION: You have a plate of 45 cookies. Ten have chocolate chips and 15 have pecans. Of the cookies mentioned in the preceding sentence, 6 have both chocolate chips and pecans. You select       Log On


   

Question 1138701: You have a plate of 45 cookies. Ten have chocolate chips and 15 have pecans. Of the cookies mentioned in the preceding sentence, 6 have both chocolate chips and pecans. You select a cookie at random. What is the probability that your cookie has chocolate chips or pecans?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13215) About Me  (Show Source):
You can put this solution on YOUR website!


Of the 15 cookies with pecans, 6 have chocolate chips also, so 9 cookies have only pecans.

Of the ten cookies that have chocolate chips, 6 have pecans also, so 4 have chocolate chips only.

So, of the 45 cookies, 9 have pecans only, 4 have chocolate chips only, and 6 have both. So 19 of the 45 cookies have at least one of the two; that means the probability of picking a cookie with pecans or chocolate chips is 19/45.

Answer by ikleyn(52914) About Me  (Show Source):
You can put this solution on YOUR website!
.

            Below is another solution,  which leads to the same answer. 


To answer the question, we need to know the number of cookies that have chocolate chips OR Pecans.


For it, add the numbers 10 and 15 that are known as containing chocolate chips or pecans, respectively.


But doing this way, we count TWICE that 6 cookies that contain BOTH chocolate chips and pecans.


Therefore, we should subtract that 6 from the sum of 10 and 15, and doing so, we obtain the exact number of cookies

that have  chocolate chips OR pecans


    10 + 15 - 6 = 19.


Now the probability under the question is  19%2F45.


            In probabilistic terms 

We have a subset  "C"  of cookies with chocolate chips - it has 10 elements and the probability to chose from it is  p(C) = 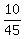10%2F45.


We have a subset  "P"  of cookies with pecans          - it has 15 elements and the probability to chose from it is  p(P) = 15%2F45.


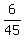We have a  subset  "CP"  of cookies with chocolate chips AND pecans - it has 6 elements and the probability to chose from it is  p(CP) = 6%2F45.


    Note that subset  "CP"  is exactly the intersection of subsets  "C"  and  "P" :  CP = (C & P).


Then the basic formula of the Probability theory says that


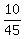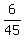    p(C U P) = p(C) + p(P) - p(C & P) = 10%2F45 + 15%2F45 - 6%2F45 = 19%2F45.

Thus both approaches give the same result.

--------------

The lesson to learn from my post is THIS : 

    1.  If  P  and C  are two subsets of the finite universal set U, then the numbers of elements in sets

        C,  P,  (C U P)  and  (C & P)  (intersection) are connected by the identity

            n(C U P) = n(C) + n(P) - n(C & P).    (1)



    2.  In the same situation, probabilities are connected by the identity


            p(C U P) = p(C) + p(P) - p(C & P).    (2)


The formulas  (1)  and  (2)  are  always  valid :   they are  UNIVERSAL.


--------------

See the lesson
    - Counting elements in sub-sets of a given finite set
in this site.